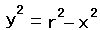球体の体積
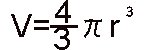
中学生の時に学習した球体の体積の公式です。この公式を覚えるため
にゴロ合わせがあって「身(3)の上に心(4)配がある(r)」とかいうのを覚え
た記憶があります。球の体積は
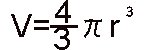
とわかっている人は多くても、それがなぜか説明できる人は少ないと思
います。
まずxy座標上の円で考えます。図①です。半径がrで、中心は原点にあ
ります。この円を表す式は

です。ではこの円をどうやって球体にするかですが、この円をx軸を中
心にして回転させます。そうすると図②のような球体ができますね。
ここから実際に球体の体積を求めるわけですが、まず図③に注目で
す。円をx軸に関して回転させた球体を、y軸に平行にスパッと切りま
す。そうすると、その切り口はどこを切っても円の形をしていますよ
ね。ハムのような薄さの円をいくつも積み重ねることで、球体ができ
ます。この円の半径はyですから円の面積は
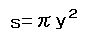
です。この円をrから(-r)の範囲まで積み重ねるわけですから、積分しま
す。積分を式で表すと

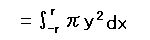 ・・・Ⅰ
・・・Ⅰ
です。

より
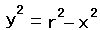
これをⅠ式に代入して、

となります。
それにしても、もし中学生から「なぜ球体の体積の公式はああいうふう
になるんですか?」と聞かれたら、どう説明したらいいんでしょうか
ね。積分を知っている高校生ならいいんですがね。「将来の楽しみにと
っておきましょうね。」などど言って、その場を逃げるしかありません
ね(笑)。
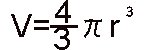
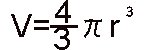
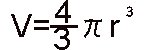

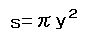

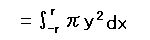 ・・・Ⅰ
・・・Ⅰ