なぜ円錐の体積は円柱の１／３なのか�A？

�@では視覚的に証明したわけですが、この章では視覚と計算の両方を

使います。まず、円錐は回転体であることに着目します。図�Aで、



をｘ軸に関して回転させます。すると�@と同じ円錐形ができますね。では

どうやって上の方程式から円錐の体積を求めるかということですが、図

�Aの円錐をｙ軸と平行となるようにスパッと包丁で切ってみます。どこを

切っても、切り口は円の形ですね。円錐を薄いハムのように切り刻ん

で、一枚ずつ見ればただの円だけれど、それをすべてくっつけると元の

円錐�@に戻りますね。

まず一枚の円の面積を求めます。図�Aより半径がｒの円ですから、面積

は



ですね。これを０〜ｈの長さ分だけ積み重ねるわけです。では積み重ね

てみようということになりますが、大学生以上の方はもうお気づきです

ね。ここで積分です。一枚の円の面積を０〜ｈの範囲で積分してやれば

いいわけですね。式は



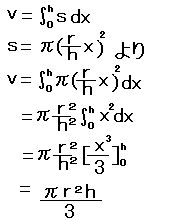
となります。円錐の体積は求まりました。円柱はというと、

（底面積)×(高さ）より



ですね。これで円錐の体積は円柱の１／３となっていることが納得いた

だけました？

ここで付け加えますと、面積を積み重ねていくと体積ができるというの

は積分において重要な考え方で、このことをカバリエリの原理とよびま

す。もっと簡単なことを言うと、一本の線をいくつも集めれば面積がで

きますね。実は１９７７年以前に生まれた人なら高校でカバリエリとい

名前は知らなくても、この考え方は習ったんですね。新課程になってか

らはなくなってしまうんです。２００２年からの新指導要領ではさらに

３割削減だとか。うーむ、確かに負担は減るでしょうが、学力はと言わ

れればちょっとね・・・という感じでしょうか。ご意見その他、メールでお

待ち申し上げます。